图像检索：Spreading Vectors for Similarity Search

Thinking in Reverse.

Spreading Vectors for Similarity Search是小白菜崇拜的Matthijs Douze和Herve Jegou的作品，发表于ICLR 2019，是一篇对思维方法非常有启发作用的paper，可能会成为利用DNN构建索引方面的经典。这样一篇因为思维的光辉而动人的paper，小白菜很乐意成为它的布道者，并希望借自己的绵薄之力，去传播、应用和改进。

主要思想

Spreading Vectors是逆向思维的一种产物。在我们设计量化器的时候，通常是将量化器适配到待量化数据（分布）上，而很少或者说没有考虑过逆向设计的可能性，即将数据（分布）适配到预先设定的满足某种分布的量化器上。这种正向思维的方式，产生了很多经典的向量索引方法，比如PQ及其变种、ITQ等，但近些年来，除了基于图ANN创造了像HNSW这样非常work的方法外，矢量量化方法给小白菜的感觉是止步不前，没有很出彩很work的工作，大部分工作都停留于修修补补，或者说虽然有一些表现还不错，但很难推广应用的方法。其中缘由，小白菜以为，思维的困局是其中很重要一个原因。技术相对比较容易实现，但思维的困局，往往很难打开。Spreading Vectors思维的光辉正体现在这里，它采用逆向思维的方式，对数据分布重新进行调整，将其投影到均匀分布的空间，然后采用$sign()$二值量化器或格子量化器进行量化，从而完成索引的构建。

在对数据分布重新进行调整，有两个基本要求：

近邻关系尽可能得到保持，不能破坏数据在原始空间中的近邻关系。 数据经过映射后，数据类内部尽可能呈现均匀分布（展开状态，这也是得到的vector具有spreading属性的含义），以便尽可能增大格子量化器对空间的利用率。

关于用DNN做索引结构的想法，Jeff Dean在2017年第一次用DNN尝试优化数据库索引，并发表了The case for learned index structures，但那是面向key-value的低层数据结构优化。Spreading Vectors受Jeff Dean一维数据索引的启发，将使用DNN构建索引结构的想法，拓展到向量索引上。

方法框架

Spreading Vectors索引构建过程，包含两个部分，分别为：catalyzer和discretization，如下图所示：

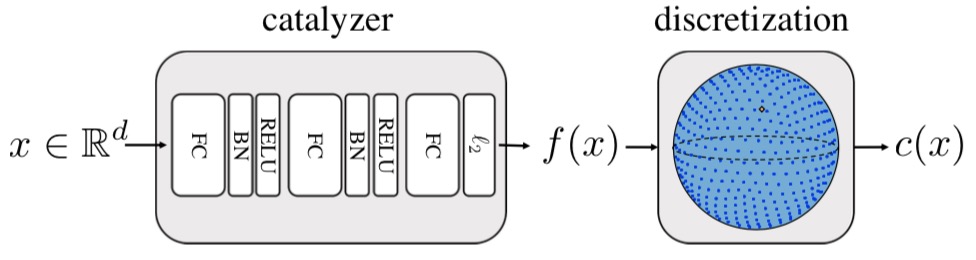
对应的作用为：

catalyzer完成原始vector到Spreading Vectors的映射，是一个3层的感知器。该3层的DNN实现数据的近邻结构保持与均匀张开，数据的张开程度，由差分熵正则项前的参数$\lambda$控制。 discretization完成Spreading Vectors的量化，可以是$sign()$或者格子量化器，完成最终数据的量化。

具体方法

从原始vector到Spreading Vectors，数据在重新映射过程中需要保持的两个基本要求，3层DNN优化的目标函数为：

\[\begin{equation} loss = loss_{rank} + \lambda loss_{KoLeo} \end{equation}\]

其中$loss_{rank}$用于保持数据在投影过程中的原始近邻关系（原始流形结构），$loss_{KoLeo}$，即差分熵，用于张开数据，使数据尽可能均匀分布在整个空间，从而加大格子量化器对空间的利用效率。我们先抛却$loss_{rank}$和$loss_{KoLeo}$的具体表示形式，观察不同的差分熵正则项参数lambda对分数分布的影响，如下图示：

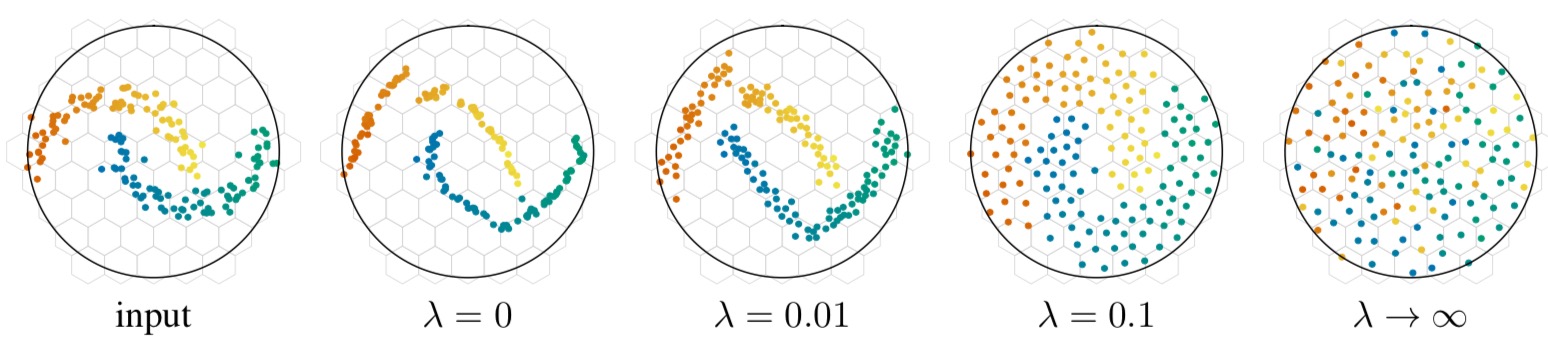
上图，格子量化器以六边形示意，可以看到当$\lambda$为0的时候，即用于张开数据的差分熵正则项完全不起作用，经过3层DNN后，数据邻近之间的关系变得更加紧致，这对于量化而言，可并不是一件好事，因为数据变得更加紧致，会导致格子量化器的利用效率变得非常低，因为有很多格子量化器，里面没有包含任何数据，这就意味着，那些包含了数据的格子量化器，需要容纳更多的数据。这样导致的问题是，容纳在同一个格子量化器的这么多的数据，我们没法再做区分了，从而导致格子量化器的利用效率非常低下。

举个更加直观的例子，比如一间客栈，有10间房子，需要容纳10个人，并且还需要很快的定位到张三在某个房间，我们有很多种分配方式，其中两种分配方式：

一人一间房子； 有些房子有多个人，某些房子是空着的；

当我们需要寻找张三的时候，第一种方式显然最快，房间号对应一下即可；但是第二种方式，在我们知道是某间房子后，由于里面存在多人，我们还是没法区分出谁是张三。这就是说，在空间利用率上，第一种方式显示是最优的，它区分数据的粒度更细。这正如PQ和哈希方法，PQ相比哈希，排序的粒度更细一样。

同时从上图我们也可以看到，当$\lambda$区域无穷大时，也就是差分熵占据主导地位的时候，数据之间的近邻关系完全被破坏，呈现出一种完全均匀分布的状态，这显然不是我们希望看到的。因而，$\lambda$参数的选取至关重要。下图是Deep 1M数据集经过catalyzer降到8维后，随机选取其中的两维的侧视图：

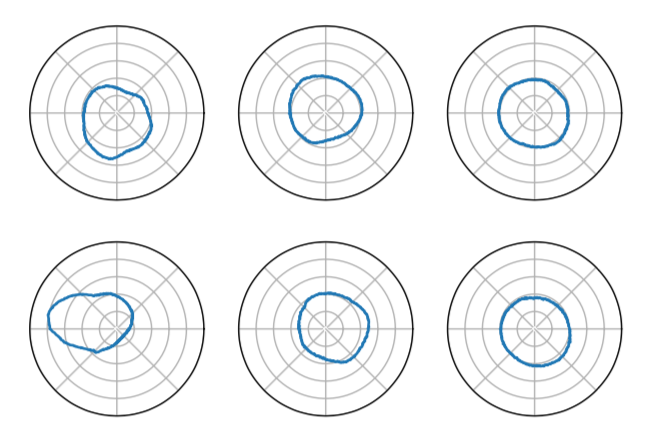
左边是$\lambda = 0$，中间是$\lambda = 0.02$，右边是$\lambda = 1.0$，相比于$\lambda = 0$，$\lambda$为0.02或1.0的时候，数据分布得均匀。另外作者还从rank@1和rank@100的距离分布，来进一步可视化验证catalyzer确实起到了很好的作用。

$loss_{KoLeo}$的具体表达形式，可以细看论文推导，我们重点一下$loss_{rank}$以及训练过程。

训练过程

$loss_{rank}$作者采用的是典型的triplet loss，因而整个过程的训练，涉及到三元组怎么训练的问题。回到前面强调过的，Spreading Vectors对数据分布重新进行调整的时候，有两个基本的要求，即原始空间近邻关系尽可能得到保持，因而对于每一个样本$x_{i}$，作者将原始空间中的$top@k_{pos}$的最近邻，作为该数据点(anchor)的正样本（正样本不再更新），catalyzer的输出$f(x_{i})$的$top@k_{neg}$作为负样本，负样本的更新在每跑完一个epoch后重新计算，然后更新。

超参影响

涉及到的超参主要是$lambda$、$k_{pos}$、$k_{neg}$以及$f(x_{i})$输出的维度$d_{out}$，作者发现，$k_{pos}$和$k_{neg}$，对结果的影响不是很大，文中作者将其$k_{pos}$设置为10，$k_{neg}$设置为50。对于固定的编码位，$d_{out}$主要影响特征表达的好坏与压缩编码的难以程度。在训练的过程中，这些参数的设置，可以参考论文中得出的经验。

实验结果

跟PQ、OPQ相比，有了比较大的提升，编码的时间，跟OPQ相比，并没有显著的耗时增加，主要是设计的catalyzer是一个3层的DNN轻量级网络。在二值量化上，召回率相比ITQ也有了较好的提升。

Spreading Vectors一个非常好的特征是，由于catalyzer是一个特征学习器，所以可以将Spreading Vectors作为特征的预处理过程，加到不同索引方法的前级，来boost索引的召回。

启发

Spreading Vectors是DNN度量学习的产物，并结合量子量化器等量化方式，为采用神经网络构建索引，打开了新的思路，后面应该会有很多在这个基础上不断改进、拓展的方法出现。其逆向思维、$loss_{KoLeo}$、格子量化、以及如何使用无监督的方式构造非常吻合数据映射要求的方法，都值得喝彩。