高数必记的函数图像

引言：本文的五个函数图像，是宇哥要求我们必须得记住的。我把它们各自的周长、面积等特性也附在一旁，以供复习。

心形线

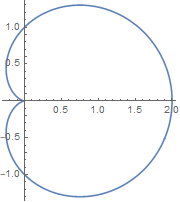
极坐标方程: \( \; r = a\,(1+\cos \theta), \, \theta \in [\, 0, \pi \,] \)

周长: \( \; \frac{1}{2}L = 4a\)

面积: \( \; \frac{1}{2}S = \frac{3}{4}\pi a^2 \)
注: 图中 a = 1, \( \theta \in [\, 0, 2\pi \,] \)

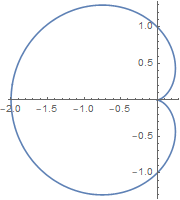
极坐标方程: \( \; r = a\,(1- \cos \theta),\, \theta \in [\, 0, \pi \,] \)

周长: \( \; \frac{1}{2}L = 4a\)

面积: \( \; \frac{1}{2}S = \frac{3}{4}\pi a^2 \)
注: 图中 a = 1, \(\, \theta \in [\, 0, 2\pi \,] \)

双扭线

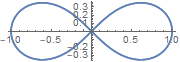
极坐标方程:\(\; \rho ^2 = a^2 \cos 2\theta, \, \theta \in [\, 0, \frac{\pi}{4}\,] \)

直角坐标方程: \(\; (x^2+y^2)^2 = a^2(x^2-y^2)\)

周长: 周长我求不出来啊,哪位老哥会求，在下面留言告诉我吧~

面积: \(\; \frac{1}{4}S = \frac{1}{4}a^2 \)
注: 图中 a = 1, \(\, \theta \in [\, 0, 2\pi \,] \)

摆线

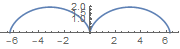
参数方程: \; \begin{cases} x = r\,(t-\sin t), \\ y = r\,(1-\cos t), \end{cases} \quad t \in [\, 0, \pi \,]

周长: \(\; L = 4r \)

面积: \(\; S = \frac{3}{2}\pi ^2 \)
注: 图中 r = 1，\(\; t \in [\, -\pi, \pi \,]\; \)

星形线

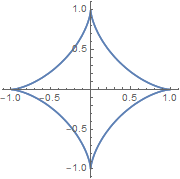
直角坐标方程: \(\; x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}} \;\)

参数方程:\; \begin{cases} x = a \, {\cos t}^3, \\ y = a \,{\sin t}^3, \end{cases} \quad t \in [\, 0, \frac{\pi}{2} \,] \;

周长:\(\; \frac{1}{4}L = \frac{3}{2}a \;\)

面积:\(\; \frac{1}{4}S = \frac{3}{32}\pi a^3 \;\)
注: 图中 a = 1, \( t \in [\, 0, \, 2\pi \,] \)

事实证明，Mathematica 在画图这方面还是比 Matlab 要舒服很多的。这个软件上手很快，学个几分钟，一般的函数图像就完全可以搞定了！哈哈！
还有一点，这几个函数，我都只写了它们的部分表现形式，并没有把各自的 直角坐标方程、极坐标方程以及参数方程 都写出来，是因为考题中出现的也就是我给出的这几种形式。

推荐阅读: 记不住的高数公式